Trong bài viết này, ta sẽ tìm hiểu về các phép đo độ tương đồng để hiểu được hai vector embedding được gọi là tương tự nhau thật sự có nghĩa là gì.
Trong bảng dưới đây là các phép đo độ tương đồng mà ta sắp tìm hiểu và các tính chất của chúng ảnh hưởng đến phép đo.
| Phép đo | tính chất |
|---|---|
| Khoảng cách Euclid | Hướng và độ lớn |
| Độ tương tự cosine | Hướng |
| Tích vô hướng | Hướng và độ lớn |
Khoảng cách Euclid
Khoảng cách euclid là khoảng cách trên một đường thẳng giữa 2 vector trong không gian đa chiều.
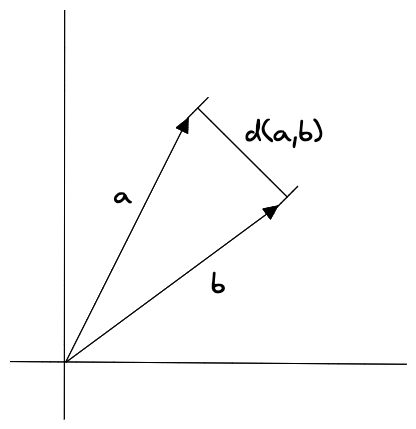
Công thức tính khoảng cách Euclid giữa 2 vector a và b:
\[d(a,b) = \sqrt{(a_1-b_1)^2+(a_2-b_2)^2+...+(a_n-b_n)^2}\]Để tính khoảng cách giữa 2 vector a và b, đầu tiên ta sẽ tính hiệu của các phần tử trong mỗi vector tương ứng với nhau ($a_1$ và $b_1$, $a_2$ và $b_2$,..) , sau đó sẽ lấy tổng bình phương của các hiệu này, căn bậc hai của tổng này chính là kết quả cuối cùng.
Phép đo này dễ bị ảnh hưởng bởi độ lớn của mỗi vector, có nghĩa là những vector có các phần tử lớn sẽ có khoảng cách euclid lớn hơn so với các vecctor có các phần tử nhỏ, dù rằng những vector này đều được xem là tương đồng với nhau. Điều này có thể được biểu diễn bằng công thức:
\[d(\alpha x, \alpha y) = \alpha d(x,y)\]Khoảng cách euclid có thể được hiểu đơn giản rằng, nếu 2 vector có khoảng cách euclid rất nhỏ, thì có nghĩa là các thành phần tương ứng của mỗi vector sẽ rất gần nhau.
Khoảng cách euclid không được ưa chuộng đối với các mô hình deep learning mà thường được sử dụng đổi với thuật toán mã hóa vector đơn giản hơn như Locality Sensitive Hashing. Vì tính chất đơn giản của nó, hãy tận dụng nó trong các trường hợp mà bạn cảm thấy nó có thể phát huy hiệu quả của mình thay cho các phương pháp phức tạp hơn.
Tích vô hướng
Công thức tích vô hướng quen thuộc của hay vector a và b:
\[\mathbf a \cdot \mathbf b = \sum_{i=1}^n a_i b_i = a_1 b_1 + a_2 b_2 +..+a_n b_n\]một công thức tương tự khác, tích vô hướng có thể được tính bằng tích độ lớn giữa 2 vector và góc cosin giữa chúng
\[\mathbf a \cdot \mathbf b = \lvert \mathbf a\rvert \lvert \mathbf b \rvert cos \alpha\]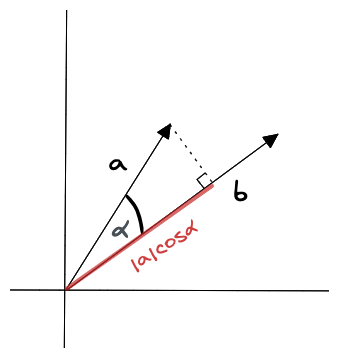
Tích vô hướng là một giá trị vô hướng, có nghĩa là nó chỉ là một số chứ không phải một vector. Tích vô hướng dương khi góc giữa 2 vector nhỏ hơn 90 độ, âm khi góc giữa 2 vector lớn hơn 90 độ, bằng 0 khi 2 vector vuông góc với nhau.
Tích vô hướng có thể bị ảnh hưởng bởi cả độ lớn và hướng của vector. Khi 2 vector có cùng độ lớn nhưng khác hướng, tích vô hướng sẽ lớn hơn nếu 2 vector cùng chỉ về một hướng và sẽ nhỏ hơn nếu chỉ về hướng khác nhau.
Tích vô hướng thường được sử dụng trong các mô hình ngôn ngữ lớn, một vài mô hình như msmarco-bert-base-dot-v5 chỉ cho phép sử dụng tích vô hướng mà không phải là các phép đo nào khác.
Tích vô hướng cũng hay được sử dụng để đánh giá độ tương đồng giữa user item và candidate item trong hệ thống đề xuất, các mô hình dựa vào collaborative filering và matrix factorization, mô hình two-tower network (sau này sẽ có các bài viết về chủ đề này).
Độ tương tự cosine
Độ tương tự cosine được tính bằng cách lấy tích vô hướng giữa 2 vector chia cho tích của độ dài 2 vector. Phép đo này không bị ảnh hưởng bởi độ lớn của vector mà chỉ là góc giữa chúng. Có nghĩa là các vector có cái giá trị lớn hay nhỏ sẽ đều có độ tương tự cosine là như nhau miễn là chúng đều có hướng giống nhau. Công thức:
\[sim(\mathbf a, \mathbf b) = \frac{\mathbf a \cdot \mathbf b}{\lVert\mathbf a \rVert \cdot \lVert \mathbf b\rVert}\]$ \lVert \mathbf a \rVert$ và $\lVert\mathbf b\rVert$ chính là độ dài của vector. Độ tương tự cosine có giá trị nằm trong khoảng từ -1 đến 1, 1 là khi góc giữa 2 vector là 0 (tức là 2 vector rất sát nhau), 0 là khi chúng vuông góc, và -1 là khi 2 hướng của chúng đối nghịch nhau.
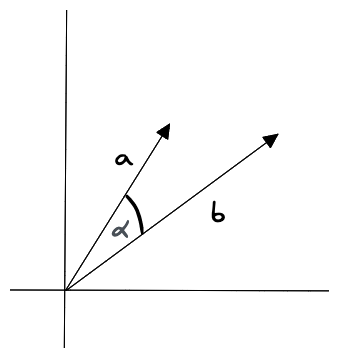
Nếu một mô hình được huấn luyện sử dụng độ tương tự cosine, bạn có thể sử dụng phép đo này hoặc cũng có thể chuẩn hóa vector rồi sử dụng tích vô hướng. 2 hướng đi này đều khả thi, trong vài trường hợp, việc chuẩn hóa rồi sử dụng tích vô hướng cho ra kết quả tốt hơn.
Ví dụ trong bài toán nhận dạng khuôn mặt, mỗi khuôn mặt sẽ có một vector embedding của nó và sẽ sử dụng phép đo cosine này để tìm ra khuôn mặt gần giống nhất trong tập dữ liệu đã đăng ký trước.
Độ tương tự cosine sẽ không phù hợp khi mà độ lớn của vector đóng vai trò quan trọng, ví dụ như sẽ là sai lầm nếu chúng ta so sánh độ tương đồng giữa vector embedding của 2 bức ảnh dựa vào mật độ pixel của chúng.
Tổng kết
Công thức chung để lựa chọn một phép đo phù hợp cho bài toán vector database indexing đó là sử dụng chính các phép đo mà đã được sử dụng để huấn luyện mô hình. Hoặc bạn phải thử nghiệm để tìm ra một phép đo khác mà có thể cho ra một kết quả thậm chí là tốt hơn.